CosmoStat specialises in the development of software and algorithms that implement cutting edge statistical methods for analysis of various types of data. The emphasis is to find new and interesting data driven approaches to solving complicated problems. The following sections summarise some of the primary interests within the group.
Sparsity
The most prominent tool in the CosmoStat toolbox is the concept of sparsity. A signal is said to be sparse if it can be represented in a basis or frame (e.g Fourier, Wavelets, Curvelets, etc.) in which the curve obtained by plotting the obtained coefficients, sorted by their decreasing absolute values, exhibits a polynomial decay. In essence, one seeks to find a representation (or dictionary) of the signal where the majority of the coefficients are close to zero. Prior knowledge of this sparse representation can be an extremely powerful constraint for optimisation problems.
The CosmoStat team have pioneered the use of sparsity in wide range of applications with particular interest in astrophysical problems. The team have developed software for implementing standard 2D sparse dictionaries but also extended some of these representations to 3D [1][2].
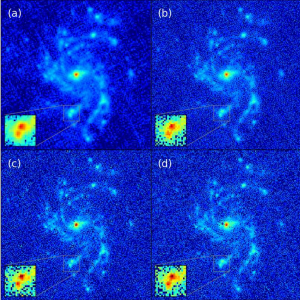
Some applications of sparsity include denoising using structured sparsity [3], the deconvolution of noisy images [4] and using inpainting to reconstruct signals with missing or corrupted data [5].
In the context of astrophysics, CosmoStat members have utilised sparsity for:
- Sparse Representations:
- Multiscale Geometric Decompositions ( Ridgelets & Curvelets, in 3D).
- 2D Wavelets and Curvelets on the sphere and 3D Wavelets on the sphere.
- Polarized Wavelets and Curvelets.
- Dictionary Learning.
- 3D Fourier-Bessel analysis.
- Wavelet Helmholtz Decomposition.
- Components Separation & Morphological Component Analysis (MCA).
- Inpainting and applications in Cosmology (CMB, CMB lensing, Weak Lensing, Galaxies surveys) and asteroseismology.
- Analysis of CMB maps: Primordial power spectrum reconstruction, non-Gaussianity , measuring the Integrated Sachs-Wolfe Effect.
- Spectroscopic redshift estimation.
- PSF estimation and image restoration.
- Analysing radio interferometric data.
- The detection of type Ia supernovae.
- Weak lensing mass mapping in 2D and 3D.
Source Separation
Accurately isolating a single source in a mixed signal in a fully automated way can be extremely challenging. Solving this problem, however, can be essential for analysing certain types of data.
One technique developed at CosmoStat to address source separation is Morphological Component Analysis [6], which implements sparsity as a tool to differentiate several contributions in a signal, each one having a specific morphology. This technique has be applied to the problem of detecting type Ia supernovae.
Another effective mathematical method for solving problems of this type is Blind source separation (BSS), which models the data as the linear combination of elementary sources or components.
The CosmoStat team have developed a Generalized Morphological Component Analysis (GMCA) algorithm that allows for the separation of sources which are sparse in any signal representation (orthonormal, redundant, etc.). It has been shown to be quite robust and performs very well at processing noisy data [7][8][9]. Extensions have been added which deal with hyper-spectral data, local mixture models, outliers and non-negative data [10][11][12].
In particular, the GMCA technique has been very successful when applied to the analysis of CMB data.
Compressed Sensing
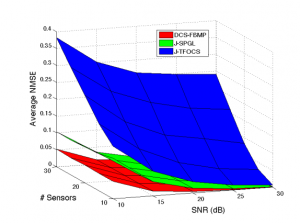
The Shannon-Nyquist theorem dictates that a minimum number of samples need to be acquired in order to fully reconstruct a signal. Compressed Sensing (CS) exploits the principles of sparsity to find a representation of the data in which fewer samples are required. The CosmoStat team have developed CS algorithms and used them for optimising the acquisition of astrophysical data [13]. Applications to projects like Herschel were shown to be extremely effective [14][15].
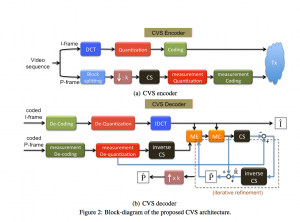
Members of CosmoStat have also employed the principles of CS to problems like the compression of video files or Compressive Video Sensing (CVS) [16]. The CVS approach has been shown to be capable of achieving high quality video reconstruction and can even be used for the classification of video sequences [17][18].
Another CosmoStat application of CS was the introduction of a new technique for range imaging (i.e. determining the distance and location of certain points in a map). The new approach reduces the number of frames required for the reconstruction of a depth map [19].
Other Topics
Wireless Sensor Networks (WSN)
Wireless Sensor Networks (WSN) are autonomous sensors that are spread around a given space to take measurements of environmental conditions.
Members of CosmoStat have developed novel techniques involving sparsity and Bayesian Matching Pursuit algorithms to perform joint reconstruction of WSN signals [20].
Additional work was done to improve mobile user localisation [21][22].