3D mass mapping

With the advent of large, high-resolution and multi-wavelength weak lensing surveys, it has recently become possible to use photometric redshift information to reconstruct the dark matter distribution in three dimensions. However, existing linear methods developed to reconstruct the 3D dark matter distribution suffer from a number of caveats which have limited their use as cosmological probes.

The GLIMPSE algorithm

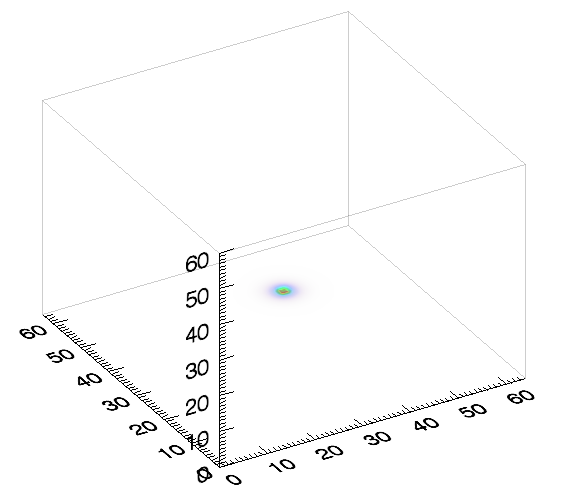
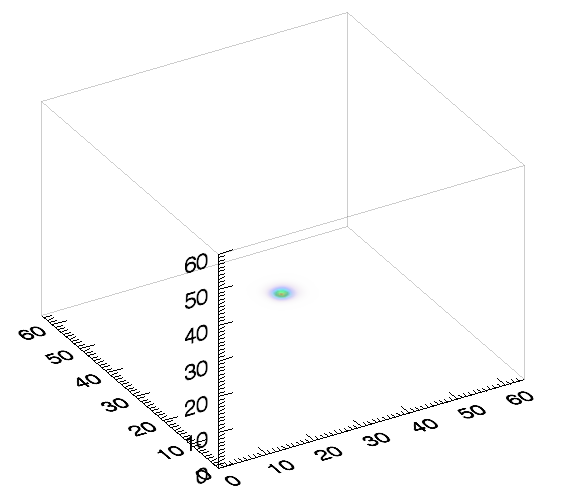
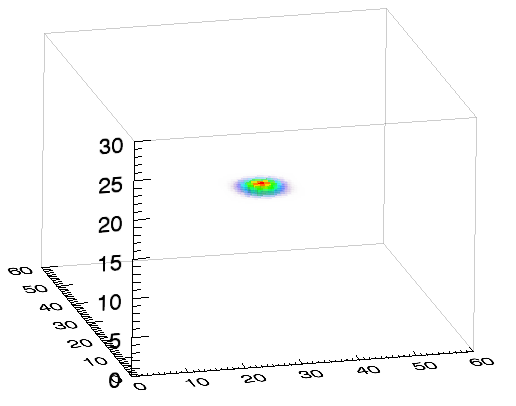
GLIMPSE is a new sparsity-based, non-linear reconstruction technique which allows for significantly more accurate mapping of the 3D dark matter distribution. Moreover contrary to other methods, GLIMPSE recovers the dark matter over-density which can be used to constrain the masses of structures.

Reconstruction of an NFW dark matter halo using GLIMPSE.
From left to right: input density contrast, reconstruction and central lines of sights (black: input, orange: reconstructed)

The 3D lensing problem is an ill-posed linear inverse problem which we address through the framework of sparse regularisation. This framework allows for accurate and robust recovery by leveraging a sparsity prior on the signal to recover (i.e. it is assumed that it can be represented using a small number of coefficients in an adapted dictionary).

We design an appropriate dictionary for the density contrast by combining Diracs along the line of sight and Isotropic Undecimated Wavelets in the 2D plane. Indeed, we expect structures to be contained on single redshift bins but roughly isotropic in the tangential plane.

Back-projection of a single active coefficient in the dictionary

The recovery of the dark matter distribution is performed by solving the following optimization problem:

$$\min\limits_{\alpha}\quad\frac{1}{2} \underbrace{\parallel \Sigma^{-1/2} [ \gamma – \mathbf{R} \Phi \alpha] \parallel^{2}_{2}}_{\mbox{data fidelity term}} + \lambda \underbrace{\parallel \alpha \parallel_{1}}_{\mbox{sparsity promoting term}}$$

where $$\alpha$$  are the coefficients of the reconstructed signal $$\delta$$ in the dictionnary $$\Phi$$, $$\Sigma$$ is the covariance matrix of the shear measurements $$\gamma$$ and $$\mathbf{R}$$ is the 3D lensing operator.

We solve this optimization problem by adapting the Fast Iterative Soft Thresholding Algorithm (FISTA) introduced in Beck and Teboulle (2009).

Results on cluster simulations

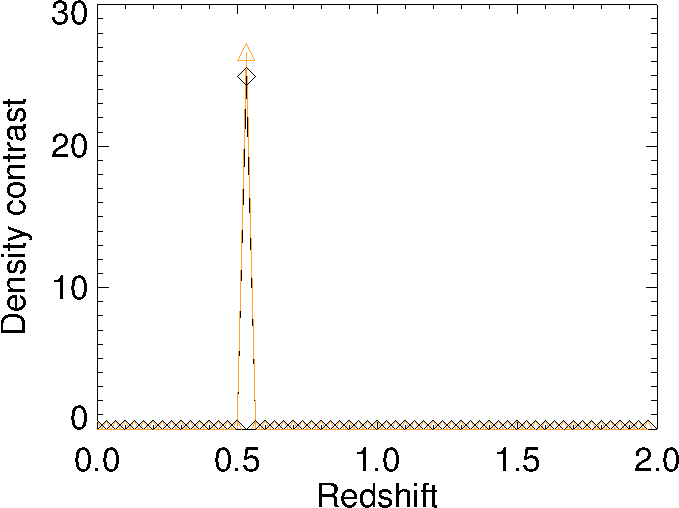
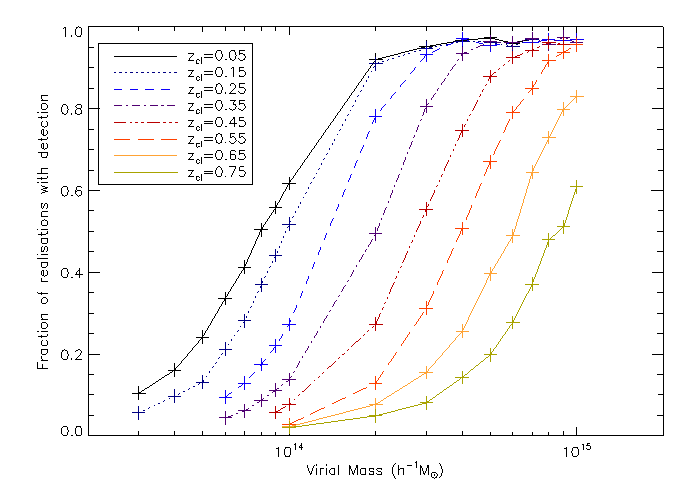
To assess the performance of GLIMPSE, we have performed a thorough statistical study on single cluster shear simulations spanning a range of redshifts between 0.05 and 0.75 and virial masses in the range $$3 \times 10^{13} h^{-1}M_{\odot} \leq M_{vir} \leq 10^{15}h^{-1} M_{\odot} $$. Results from this analysis are presented in Leonard et al. (2013).

Detection fraction of the clusters as a function of mass for different redshifts.
Detection fraction of the clusters as a function of mass for different redshifts.

Publications