Cosmological constraints with weak-lensing peak counts and second-order statistics in a large-field survey
| Authors: | A. Peel, C.-A. Lin, F. Lanusse, A. Leonard, J.-L. Starck, M. Kilbinger |
| Journal: | A&A |
| Year: | 2017 |
| Download: | ADS | arXiv |
Abstract
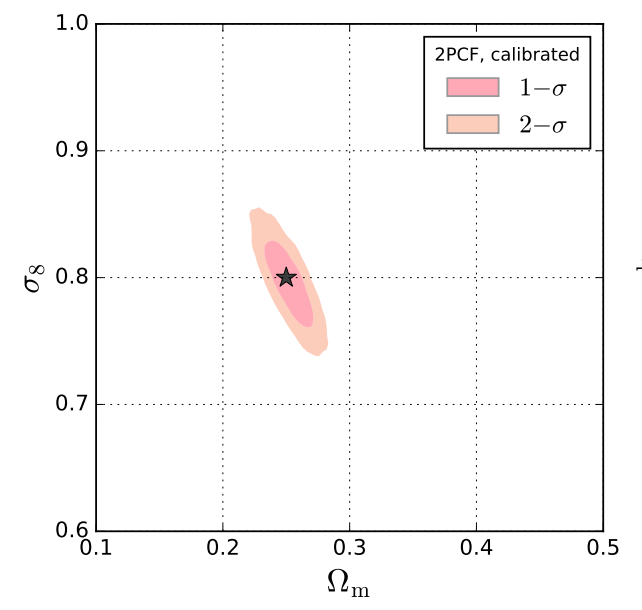
Peak statistics in weak-lensing maps access the non-Gaussian information contained in the large-scale distribution of matter in the Universe. They are therefore a promising complementary probe to two-point and higher-order statistics to constrain our cosmological models. Next-generation galaxy surveys, with their advanced optics and large areas, will measure the cosmic weak-lensing signal with unprecedented precision. To prepare for these anticipated data sets, we assess the constraining power of peak counts in a simulated Euclid-like survey on the cosmological parameters Ωm, σ8, and w0. In particular, we study how the Camelus model--a fast stochastic algorithm for predicting peaks--can be applied to such large surveys. We measure the peak count abundance in a mock shear catalogue of ~5,000 sq. deg. using a multiscale mass map filtering technique. We then constrain the parameters of the mock survey using Camelus combined with approximate Bayesian computation (ABC). We find that peak statistics yield a tight but significantly biased constraint in the σ8-Ωm plane, indicating the need to better understand and control the model's systematics. We calibrate the model to remove the bias and compare results to those from the two-point correlation functions (2PCF) measured on the same field. In this case, we find the derived parameter Σ8=σ8(Ωm/0.27)^α=0.76−0.03+0.02 with α=0.65 for peaks, while for 2PCF the value is Σ8=0.76−0.01+0.02 with α=0.70. We therefore see comparable constraining power between the two probes, and the offset of their σ8-Ωm degeneracy directions suggests that a combined analysis would yield tighter constraints than either measure alone. As expected, w0 cannot be well constrained without a tomographic analysis, but its degeneracy directions with the other two varied parameters are still clear for both peaks and 2PCF.