| Authors: | C. Lin, M. Kilbinger, S. Pires |
| Journal: | A&A |
| Year: | 2016 |
| Download: | ADS | arXiv |
Abstract
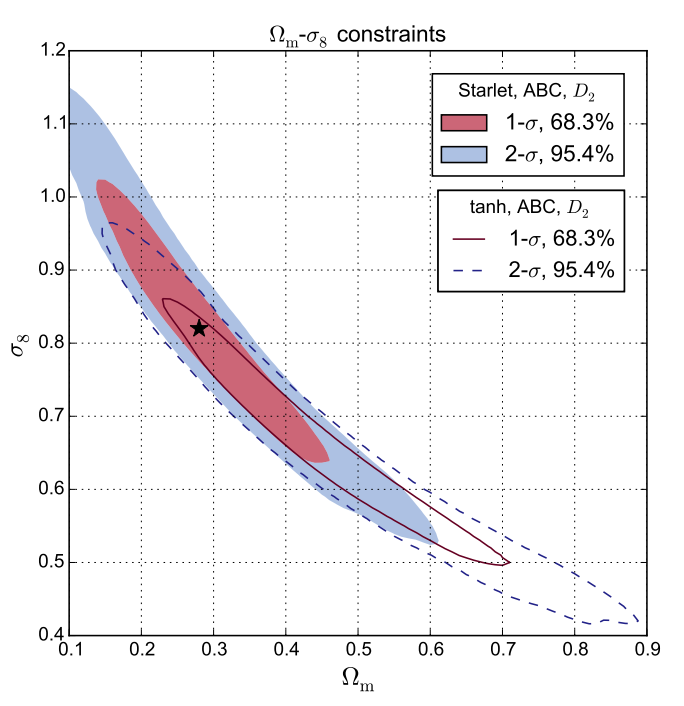
This is the third in a series of papers that develop a new and flexible model to predict weak-lensing (WL) peak counts, which have been shown to be a very valuable non-Gaussian probe of cosmology. In this paper, we compare the cosmological information extracted from WL peak counts using different filtering techniques of the galaxy shear data, including linear filtering with a Gaussian and two compensated filters (the starlet wavelet and the aperture mass), and the nonlinear filtering method MRLens. We present improvements to our model that account for realistic survey conditions, which are masks, shear-to-convergence transformations, and non-constant noise. We create simulated peak counts from our stochastic model, from which we obtain constraints on the matter density Ωm, the power spectrum normalisation σ8, and the dark-energy parameter w0. We use two methods for parameter inference, a copula likelihood, and approximate Bayesian computation (ABC). We measure the contour width in the Ωm-σ8 degeneracy direction and the figure of merit to compare parameter constraints from different filtering techniques. We find that starlet filtering outperforms the Gaussian kernel, and that including peak counts from different smoothing scales helps to lift parameter degeneracies. Peak counts from different smoothing scales with a compensated filter show very little cross-correlation, and adding information from different scales can therefore strongly enhance the available information. Measuring peak counts separately from different scales yields tighter constraints than using a combined peak histogram from a single map that includes multiscale information. Our results suggest that a compensated filter function with counts included separately from different smoothing scales yields the tightest constraints on cosmological parameters from WL peaks.