| Authors: | C. Lin, M. Kilbinger |
| Journal: | A&A |
| Year: | 2015 |
| Download: | ADS | arXiv |
Abstract
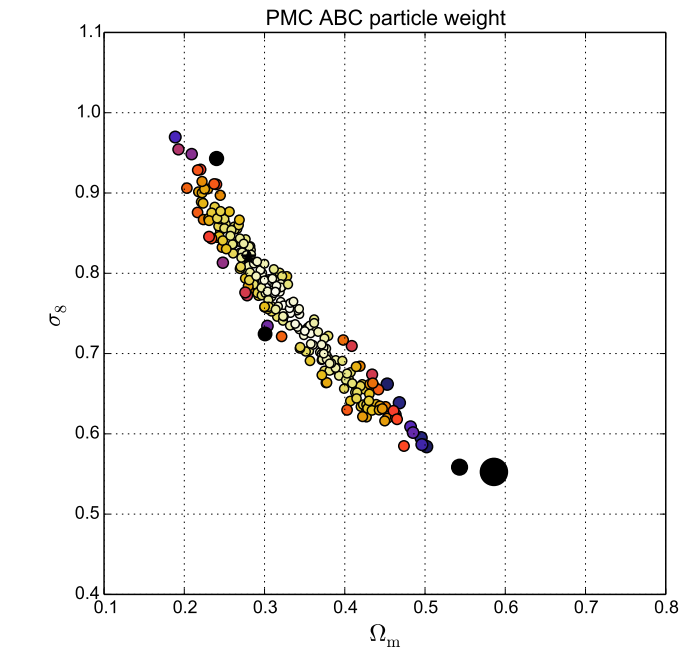
Peak counts have been shown to be an excellent tool to extract the non-Gaussian part of the weak lensing signal. Recently, we developped a fast stochastic forward model to predict weak-lensing peak counts. Our model is able to reconstruct the underlying distribution of observables for analyses. In this work, we explore and compare various strategies for constraining parameter using our model, focusing on the matter density Ωm and the density fluctuation amplitude σ8. First, we examine the impact from the cosmological dependency of covariances (CDC). Second, we perform the analysis with the copula likelihood, a technique which makes a weaker assumption compared to the Gaussian likelihood. Third, direct, non-analytic parameter estimations are applied using the full information of the distribution. Fourth, we obtain constraints with approximate Bayesian computation (ABC), an efficient, robust, and likelihood-free algorithm based on accept-reject sampling. We find that neglecting the CDC effect enlarges parameter contours by 22%, and that the covariance-varying copula likelihood is a very good approximation to the true likelihood. The direct techniques work well in spite of noisier contours. Concerning ABC, the iterative process converges quickly to a posterior distribution that is in an excellent agreement with results from our other analyses. The time cost for ABC is reduced by two orders of magnitude. The stochastic nature of our weak-lensing peak count model allows us to use various techniques that approach the true underlying probability distribution of observables, without making simplifying assumptions. Our work can be generalized to other observables where forward simulations provide samples of the underlying distribution.