The phenomenon of light deflection in the presence of massive objects is denoted as gravitational lensing. This effect was measured for the first time in 1919 during a solar eclipse, showing that the apparent positions of stars on the sky change due to light deflection by the Sun’s gravitational field. This was the first successful test of Einstein’s theory of general relativity and it’s prediction of gravitational lensing.
On extra-galactic scales, galaxies, clusters of galaxies, and even the filamentary structure of the cosmic web can act as gravitational lenses. The gravity of those objects causes images high-redshift, background galaxies to be distorted. If the distortions are very small, they cannot be detected on individual galaxies, but only statistically, by averaging over a large number of galaxies, we speak of weak lensing.
Weak lensing is a powerful tool to measure masses of a variety of objects in the universe. Graviational lensing is directly sensitive to dark matter. It can measure the mass profile of galaxies out to large radii, where the light from stars and gas is too faint to be observed. It can trace the mass distribution of galaxy clusters. On even larger scales, weak lensing distortions of galaxies measure the properties of the cosmic web. By comparing the statistical properties of the resulting distortion pattern to theoretical models, we can study the expansion history of the universe, the constituencies of the cosmos including dark matter and dark energy, and the evolution of structure in the universe. Weak lensing has the potential to probe the cause of the accelerated expansion of the universe, and to distinguish between dark energy and modified gravity.
A review on cosmology from cosmic shear has been published recently, see also the companion web site.
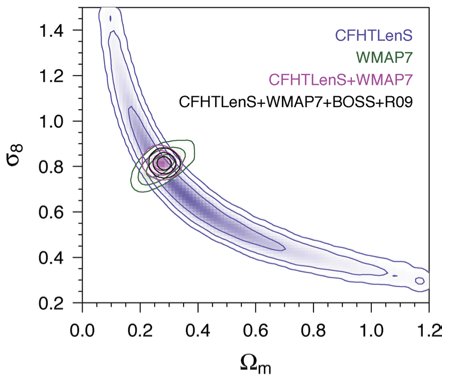 |
Cosmological constraintsMeasuring cosmological parameters and models with cosmic shear. |
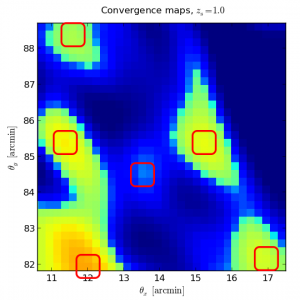 |
Peak CountingExtract non-Gaussian information from weak lensing using local maxima of mass. Model the prediction of observables with a probabilistic approach including complex observational effects. |
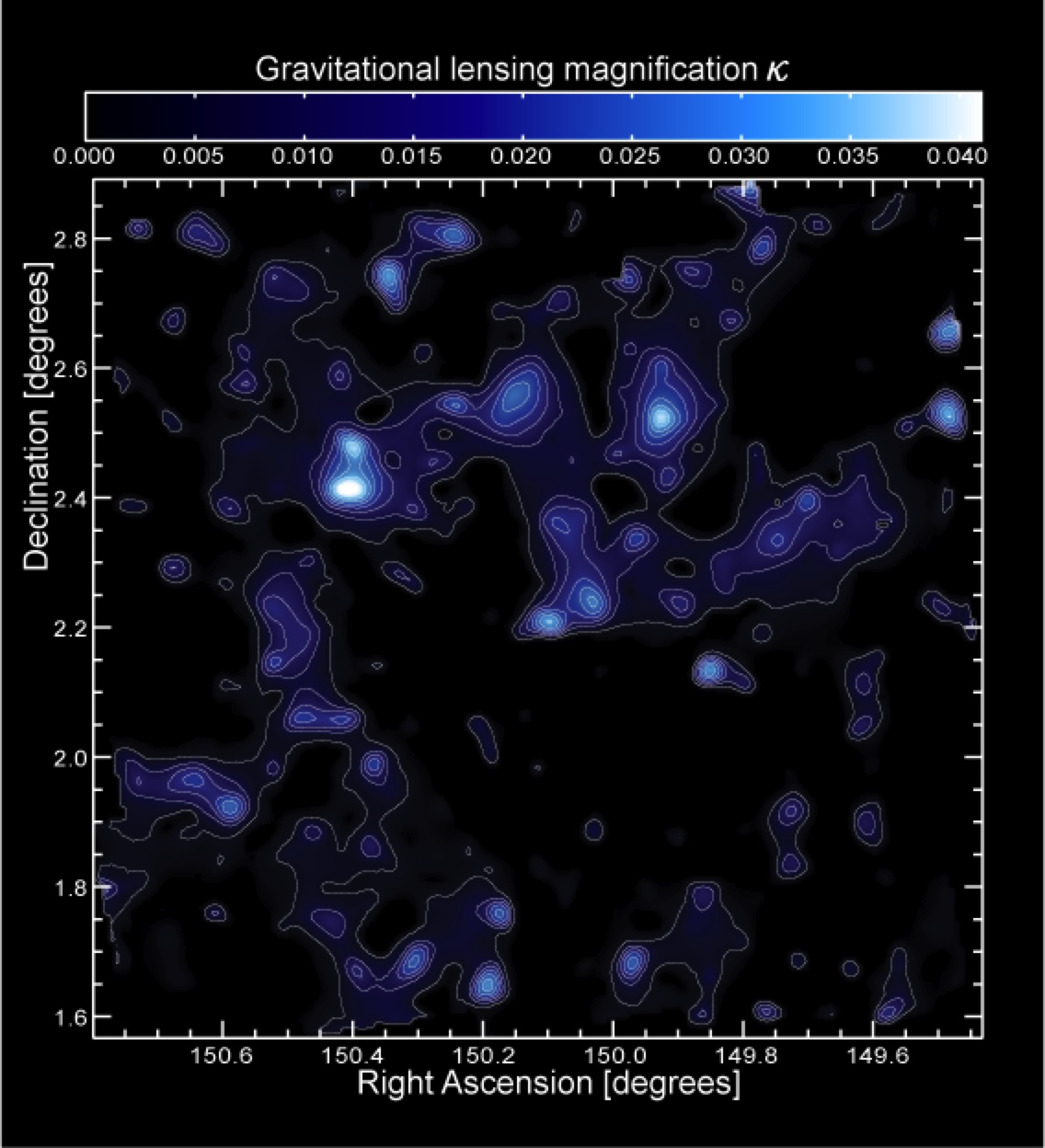 |
Reconstruction of the dark matter distribution from incomplete shear estimation. |
