Peak Counting

Fig 4 from Lin & Kilbinger (2015)
This histogram shows the agreement between $$N$$-body simulations and our model. (Fig. 4, Lin & Kilbinger 2015a)

Besides the two-point-correlation functions, peak counts from weak lensing provide an excellent tool to extract cosmological information. Peaks are local maxima of convergence maps. Therefore, they are direct tracers of massive structures. This have been shown as a powerful probe for constraining lensing-sensitive cosmological parameters, such as $$\Omega_\mathrm{m}$$, $$\sigma_8$$, and $$w$$.

In CosmoStat laboratory, we develop a stochastic approach to predict peak counts from weak lensing:

  • sample halos from the mass function,
  • compute the projected mass,
  • add noise and smooth the map,
  • create peak catalogues.
test
Constraints derived from our model, with the constant-covariance Gaussian (cg) and the varying-covariance Gaussian likelihood (vg).

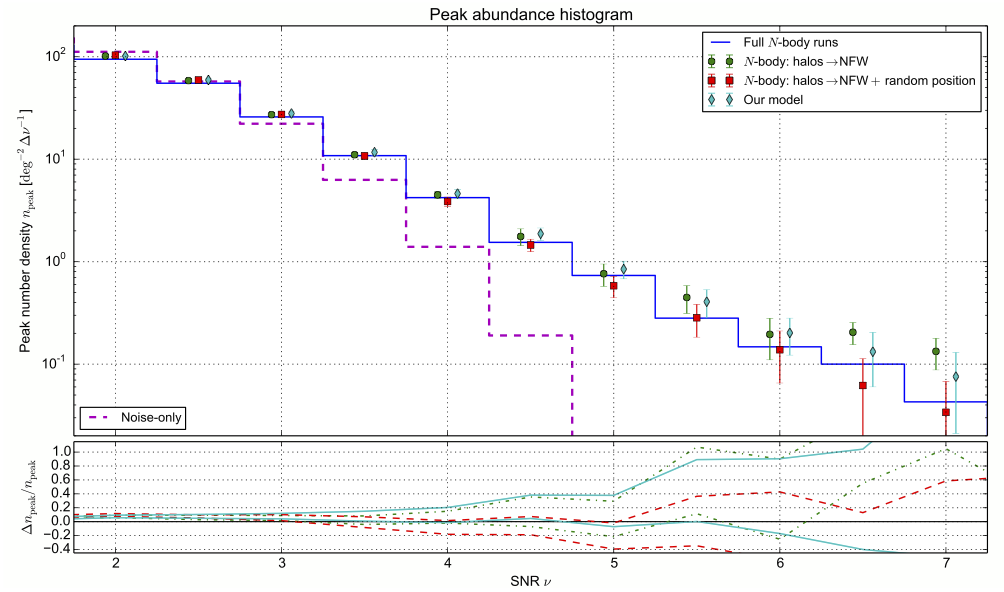
Lin & Kilbinger (2015a) have showed that the results from these fast simulations agree well with $$N$$-body runs.

There are several advantages for a fast probabilistic model of this kind:

  • The PDF of observables is well known. It is possible to examine the cosmology-dependent-covariance effect, to compute non-parametric likelihoods, or to proceed likelihood-free analysis.
  • Realistic survey settings, such as mask effects and photo-$$z$$ errors, and additional features such as intrinsic ellipticity alignment, can easily be included.
  • Economy on computation time. It only needs ~1.5 second to count peaks from a 25-squared-degree field on a single-CPU computer!

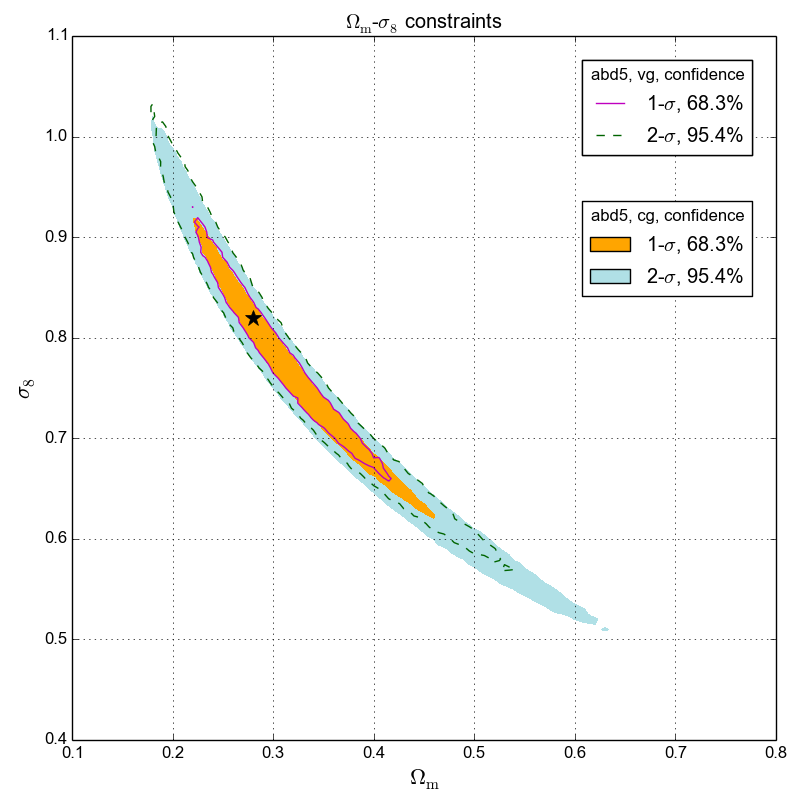
Lin & Kilbinger (2015b) have showed that supposing an invariant covariance for likelihood analysis underestimates the peak-count constraint power. It further uses Approximate Bayesian Computation (ABC) as alternative method to obtain parameter constraints, without the need to evaluate or even define a likelihood function.

The third paper in this series (Lin & Kilbinger 2016) compares different filter techniques to extract peaks from weak-lensing data (Gaussian, compensated, sparse). This work includes realistic masks and treats missing data.

This model is performed by the Camelus algorithm which is available here.

Publications