TOUSI

Blue dots show the empirical power spectrum of one realization with instrumental noise. Yellow dots show the estimated power spectrum of one of the simulated noise maps. Green dots show the the spectrum with the noise power spectrum removed. The black and red solid lines are the input and reconstructed power spectra respectively. The inner plots show a zoomed-in version.

METHOD

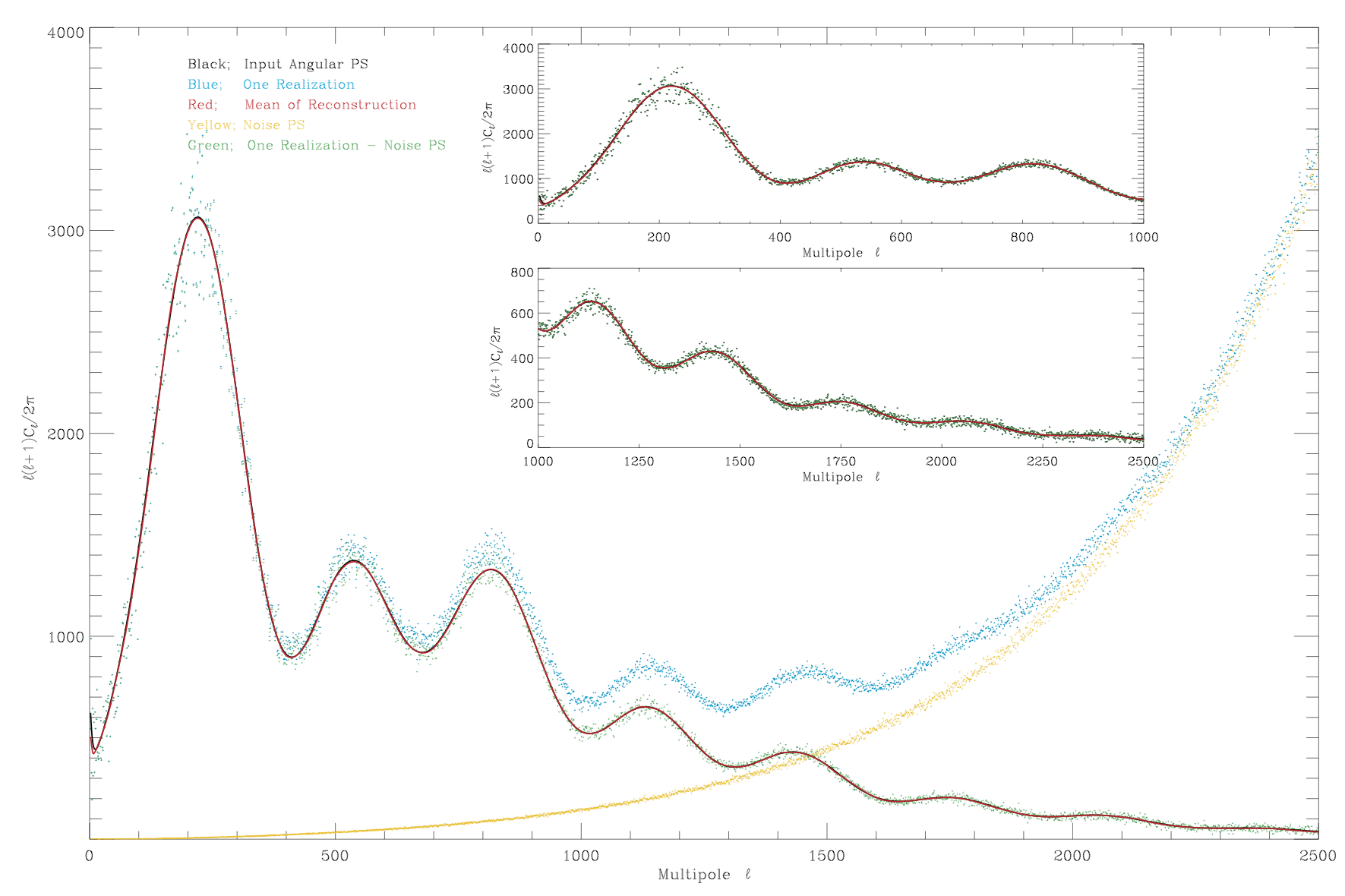
The CMB power spectrum is a powerful cosmological probe as it entails almost the entire statistical information of CMB perturbations. However, the CMB power spectrum measured by our experiments is only one realisation of the true underlying power spectrum. Consequently, even a perfect survey will be limited by cosmic variance and we can never recover the true underlying power spectrum. In addition, the noise from one realisation of the spectrum is highly non-Gaussian; it is a multiplicative chi^2-distributed noise where the degrees of freedom is scale-dependent. A proper treatment of the non-Gaussian noise of the observed power spectrum is proposed in my TOUSI algorithm, which is based on the Wahba variance stabilisation transform (VST). The VST transforms the spectrum into a space where the noise can be treated as an additive Gaussian noise with zero-mean and a unit variance.

TOUSI is a new sparsity-based, non-linear algorithm that exploits the VST and the sparsity properties of the CMB spectrum, in both wavelets and discrete cosine transform (DCT) space, to propose an estimator of the true spectrum from one realised power spectrum. This novel approach estimates the true CMB spectrum without having to know the cosmological parameters for the first time. It can be used to simulate CMB maps with similar properties as the true one without assuming any cosmology.

ALGORITHM

A signal $$X$$ considered as a vector in $$\mathbb{R}^N$$, is sparse if most of its entries are equal to zero. Generally signals are not sparse in direct space, but can be sparsified by transforming them to another domain; for eg, $$\sin(x)$$ is 1-sparse in the Fourier domain. In the so-called sparsity synthesis model, a signal can be represented as the linear expansion

\[ X =\Phi \alpha= \Sigma_{i=1}^T \phi_{i}\alpha[i], \]

where $$\alpha[i]$$ are the synthesis coefficients of $$X$$ and $$\phi_{i}$$ are called the atoms (elementary waveforms) of the dictionary $$\Phi=(\phi_{1},\ldots,\phi_{T})$$; such as Fourier (FT), wavelet (WT) and discrete cosine transforms (DCT).

The CMB power spectrum is very sparse in both the DCT and WT dictionaries, although their sparsifying capabilities are different; DCT recovers global features of spectrum (i.e. the peaks and troughs) while WT recovers localized features. These complementary capabilities of DCT and WT transforms are combined to propose a versatile way for adaptively estimating the theoretical power spectrum from a single realization. Having $$X=C[\ell]$$ and $$\widehat{S}_N[\ell]$$ as the noise power spectrum, the equation to minimize is

\[ \min_{X} | {\Phi}^{T}{X} |_1 \quad \mathrm{s.t.} \quad \begin{cases} X \geqslant 0 \\ M_d \odot \big(\Phi_d^{T}{\cal T}(X+\widehat{S}_N)\big) = M_d \odot \big(\Phi_d^{T} C^{s}\big), ~ d \in {1,\cdots,D} \end{cases} \]

which is performed iteratively;

\[ \widetilde{{X}} = {\cal R} \left( {\cal T} \left( { X}^{(n)} + \widehat{S}_N\right) + { \Phi} M \odot \left({ \Phi}^{T} \left( C^{s} -{\cal T} \left( { X}^{(n)}+\widehat{S}_N\right) \right) \right)\right) – \widehat{S}_N \]
\[ {X}^{(n+1)} = \mathcal{P}_{+}\left( { \Phi} ~ \text{ST}_{\lambda_n}({ \Phi}^{T}\widetilde{{X}}) \right) \]

CODE

The code is integrated in the iSAP software (called mrs_tousi.pro).

PUBLICATIONS